浮点数问题探究

问题

最近在使用openresty实现一些业务，业务中设计了一套二进制编码，目前为49bit。真正实现的时候发现lua里不支持(u)int64, 只有double，同时bitops也只支持32位。没有多想，直接用double存储了编码的10进制，然后开始关注如何去支持位运算。结果可想而知：

C-module for lua

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61


// bitop.c
#include <inttypes.h>
#include <lua.h>
#include <lauxlib.h>
#include <lualib.h>

static int tostring(lua_State* l) {
    int n = lua_gettop(l);
    if (n == 2) {
        uint64_t a = lua_tonumber(l, 1);
        uint64_t b = lua_tonumber(l, 2);
        //printf("%"PRIu64" %"PRIu64"\n", a, b);
        //printf("%"PRIX64" %"PRIX64"\n", a, b);
        char str[65];
        if (b == 16) {
            sprintf(str, "%"PRIx64, a);
            lua_pushstring(l, str);
        }
        if (b == 10) {
            sprintf(str, "%"PRIu64, a);
            lua_pushstring(l, str);
        }
        if (b == 2) {
            uint64_t mask = 0x8000000000000000ULL;
            int i = 0;
            for (int j = 0; j < 64; ++j) {
                if (a & mask) {
                    str[i++] = '1';
                } else {
                    if (i) {
                        str[i++] = '0';
                    }
                }
                a = a << 1;
            }
            if (i == 0) {
                str[i++] = '0';
            }
            str[i] = '\0';
            lua_pushstring(l, str);
        }
        return 1;
    }
    return 0;
}


static const luaL_Reg lib[] = {
    // {"lshift", lshift},
    // {"rshift", rshift},
    // {"band", band},
    // {"bor", bor},
    {"tostring", tostring},
    {NULL, NULL}
};

int luaopen_bitop(lua_State* l) {
    luaL_register(l, "bitop", lib);
    return 1;
}
// gcc bitop.c -std=c99 -I/usr/local/luajit/include/luajit-2.1 -fPIC -shared -o bitop.so

简单测试下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


-- test.lua
local bit = require "bitop"
local a = bit.lshift(1)
print('2^63 in dec : ', bit.tostring(2^63, 10))
print('2^63 in bin : ', bit.tostring(2^63, 2))
print('2^64 in bin : ', bit.tostring(2^64, 2))
print('0xFFFF in bin : ', bit.tostring(0xFFFF, 2))
print('0xFFFFFFFFFFFFF000 in bin : ', bit.tostring(0xFFFFFFFFFFFFF000, 2))
print('0xFFFFFFFFFFFFF000 in dec : ', bit.tostring(0xFFFFFFFFFFFFF000, 10))
print('0xFFFFFFFFFFFFF000 in hex : ', bit.tostring(0xFFFFFFFFFFFFF000, 16))
print('0xFFFFFFFFFFFFFF00 in bin : ', bit.tostring(0xFFFFFFFFFFFFFF00, 2)) 
print('0xFFFFFFFFFFFFFF00 in dec : ', bit.tostring(0xFFFFFFFFFFFFFF00, 10))
print('0xFFFFFFFFFFFFFF00 in hex : ', bit.tostring(0xFFFFFFFFFFFFFF00, 16))
print('0x0000FFFFFFFFFFFF in hex : ', bit.tostring(0x0000FFFFFFFFFFFF, 16))
print('0x000FFFFFFFFFFFFF in hex : ', bit.tostring(0x000FFFFFFFFFFFFF, 16))
print('0x00FFFFFFFFFFFFFF in hex : ', bit.tostring(0x00FFFFFFFFFFFFFF, 16))
print('0x0FFFFFFFFFFFFFFF in hex : ', bit.tostring(0x0FFFFFFFFFFFFFFF, 16))
print('0x0FFFFFFFFFFFFF00 in hex : ', bit.tostring(0x0FFFFFFFFFFFFF00, 16))
print('0x0FFFFFFFFFFFFFF0 in hex : ', bit.tostring(0x0FFFFFFFFFFFFFF0, 16))
print('0xFFF0FFFFFFFFFF00 in hex : ', bit.tostring(0xFFF0FFFFFFFFFF00, 16))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


2^63 in dec : 	9223372036854775808
2^63 in bin : 	1000000000000000000000000000000000000000000000000000000000000000
2^64 in bin : 	0
0xFFFF in bin : 	1111111111111111
0xFFFFFFFFFFFFF000 in bin : 	1111111111111111111111111111111111111111111111111111000000000000
0xFFFFFFFFFFFFF000 in dec : 	18446744073709547520
0xFFFFFFFFFFFFF000 in hex : 	fffffffffffff000
0xFFFFFFFFFFFFFF00 in bin : 	0                              -- ？？
0xFFFFFFFFFFFFFF00 in dec : 	0                              -- ？？
0xFFFFFFFFFFFFFF00 in hex : 	0                              -- ？？
0x0000FFFFFFFFFFFF in hex : 	ffffffffffff                              
0x000FFFFFFFFFFFFF in hex : 	fffffffffffff                              
0x00FFFFFFFFFFFFFF in hex : 	100000000000000                -- ？？
0x0FFFFFFFFFFFFFFF in hex : 	1000000000000000               -- ？？
0x0FFFFFFFFFFFFF00 in hex : 	fffffffffffff00
0x0FFFFFFFFFFFFFF0 in hex : 	1000000000000000               -- ？？
0xFFF0FFFFFFFFFF00 in hex : 	fff1000000000000               -- ？？

很明显是发生了溢出，但是却没有明显规律，毕竟2^63 没有溢出，但是为什么比他小的却溢出了。

之前啃CSAPP时看到过浮点数的binary形式（IEEE 754）和整型是完全不一样的，猜测肯定是lua中int64—>double有溢出/精度丢失，具体什么情况下会触发必须搞清楚，不然这套编码方案就成了纸上谈兵了。

IEEE 754

回去翻CSAPP，结合网上一些讲解，简单总结下IEEE 754里面的一些关键点

根据IEEE 754的规定，浮点数二进制计算公式为：V = (-1)^S * M * 2^E

二进制格式表示如下：

其中:

Sign(s) : 用于决定这个数是正数(s=0)还是负数(s=1)
Exponent(exp): exp = ek-1···e1e0 （二进制表示）是一个无符号数，用于编码E
- E = exp-Bias，用于对浮点数加权
- Bias = 2^(k-1) -1
Fraction(frac): n位小数字段frac = fn-1···f1f0（二进制表示）, 用于编码尾数M, 范围是1~2-ε或0~1-ε 同时：
单精度(float): K = 8, N = 23
双精度(double): K = 11, N = 52

根据exp的值，有三种不同情况的编码，用以覆盖所以情况，如下：

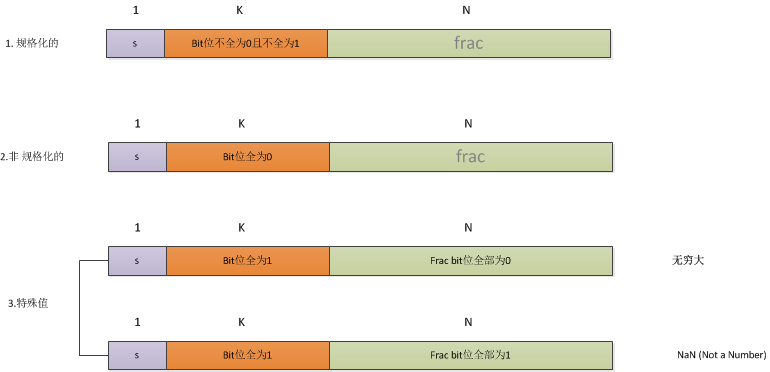
规格化的：
- 此时M的范围为1~2-ε，M = 1. fn-1fn-2···f1f0 (此为二进制表示，隐含的以1开头的 )
非规格化的：
- E = 1 - Bias
- M的范围为0~1-ε，M = 0. fn-1fn-2···f1f0
- 为什么需要非规格化，因为规格化的表示法无法表示0
特殊值：
- 可表示正无穷，负无穷，用以表示大数相乘，或者除以零时的溢出结果
- NaN 用于表示非实数，或者无穷

举个例子，将如下单精度二进制表示形式转换为浮点数表示：

因为M是隐含的以1开头的，我们在小数点前补1，小数点后按frac来排放，则M = 1.1111111(二进制)
exp = 10000110(二进制) = 134
E = exp - Bias = 134 - （2^7 - 1）= 134-127 = 7
V = 1 * 1.1111111(二进制) * 2^7 = 11111111（二进制）= 511

511逆向转为float：

511 = 2^9 - 1 = 11111111(二进制) = 1.1111111(二进制) * 2^7
因为规格化的浮点数M的取值范围为1~2-ε，则可以把511转换为1.1111111(二进制) * 2^7
则M = 1.1111111(二进制)
因为M是隐含的以1开头的，开头的1不需要存储，所以 f = 11111110000000000000000(二进制)，填充进frac
E = exp-Bias = exp - (2^7 - 1) = 7, 所以exp = 7 + 127 = 134 = 10000110(二进制)，填充进exp
511为正数，所以s位置为0

511逆向转为double：

511 = 1.1111111(二进制) * 2^7
与float相同，M = 1.1111111(二进制)
所以 f = 11111110000000000000000000000…000(53位二进制)，填充进frac
E = exp-Bias = exp - (2^10 - 1) = 7, 所以exp = 7 + 1023 = 1030 = 10000000110(二进制)，填充进exp
正数，是位置为0

问题探究

那么文章开头我们的问题，double类型究竟可以表示多大的整数，以及为什么？

根据上文的IEEE754标准，以及我们针对511的正反转换举例，可以看到，其实不管是浮点数还是整数其二进制形式其实都是存放在了frac中：

针对double，直观上看上最大可存放n+1 = 53位（加1是因为M是隐含的以1开头的，小数点前的1无需存储），即最大2^53-1
必须提到的一点是如果frac中存放不下的时候，低位会被舍弃，浮点数也会因此出现精度丢失，如果是整数则意味着被截断了
根据2我们可以看出来，如果是低位为0，被舍弃其实是不受影响的，所以2^53也是可以在double里正确表示的
同理2^63也是可以表示的 ——- 这解释了我们文章开头问题中溢出没有规律的问题
而且2^53 + 2 也是可以表示的
以此类推

所以，只能说double可以连续表达的最大的整数上限是2^53

延伸阅读

你应该知道的浮点数基础知识

我也是看了里面的举例，结合CSAPP才弄清楚浮点数的，里面的st上的那个问题非常有意思，但是文章后面的关于为何会有非规格化浮点数的原因不太苟同： “不难看出浮点数的精度和指数范围有很大关系。最低不能低过2^-7 - 1最高不能高过2^8 - 1（其中剔除了指数部分全0和全1的特殊情况）”

文章目录

问题

C-module for lua

IEEE 754

问题探究

延伸阅读